Așa cum am precizat, rezolvarea problemei de olimpiadă la matematică nu se bazează pe cunoștințe complexe în domeniul matematicii, cum ar fi formule pretențioase, ci pe modul de abordare. De fapt, această problemă care pare la început destul de complexă este o problemă simplă de geometrie, dar deghizată.

   Cea mai simplă rezolvare, pentru că au existat mai multe soluții, este prin desfășurarea cilindrului gol din carton sau a tubului gol în plan, prin care se obține un dreptunghi cu laturile de 12 cm și 4 cm. Practic, acest lucru se poate face prin tăierea rolei din carton pe lungime, pornind exact din locul unde șnurul începe să fie înfășurat. Animația următoare cred că este destul de explicită, chiar dacă nu cuprinde și momentul tăierii cu foarfeca.

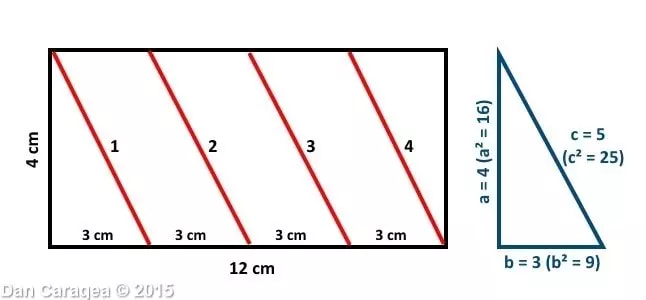
  Pentru rezolvarea problemei de olimpiadă la matematică, prin desfășurarea cilindrului înfășurat (simetric) cu șnur în plan (la două dimensiuni), se obține următoarea imagine, necesară pentru calcul:

   În dreptunghiul care a rezultat, șnurul este de fapt ipotenuza a patru triunghiuri dreptunghice. Pentru aflarea ipotenuzei unui triunghi dreptunghic se aplică o teoremă simplă, cunoscută de toată lumea, teorema lui Pitagora, care este enunțată astfel: a ² + b ² = c ², unde c reprezintă ipotenuza triunghiului. În cazul de față, cele două laturi a și b au valorile 4 și 3, iar printr-un calcul simplu rezultă că ipotenuza este de 5 cm. Șnurul fiind înfășurat simetric, de patru ori, ipotenuza triunghiului se înmulțește cu patru și am găsit lungimea totală a șnurului: 20 cm.

   În articolul cu enunțul, am precizat că este o problemă care nu necesită cunoștințe deosebite din domeniul matematicii. M-am bazat pe faptul că triunghiul dreptunghic 3-4-5 este un triunghi special, cel mai mai bine cunoscut din lume în aplicarea teoremei lui Pitagora, de care foarte mulți își aduc aminte, chiar dacă au uitat, poate, această teoremă simplă. Așa că rezolvarea era la îndemâna oricui.

   Alte teste, de logică, de inteligență sau IQ, cu sau fără imagini, și alte probleme diverse și interesante le găsiți la categoria Perspicacitate.